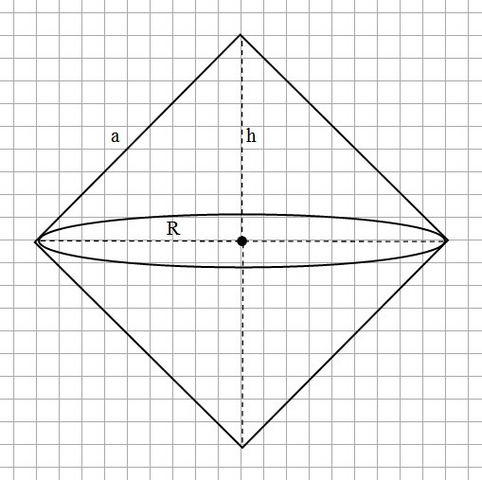
Площадь поверхности тела вращения состоит из боковых
поверхностей двух конусов с равными радиусами оснований R
и равными высотами h = R.
Боковая поверхность конуса:
S₁ = πRL = πR√(R²+h²) = πR√(2R²) = πR²√2
По т.Пифагора:
L² = R²+h² = 2R² => L = R√2 => R = (L√2)/2
Так как L = a = 3 см, то:
R = (3√2)/2 = 1,5√2 (см)
Тогда:
S₁ = πR²√2 = π*(1,5√2)²√2 = π*4,5√2 (см²)
Общая площадь тела вращения:
S = 2S₁ = 9π√2 (см²) ≈ 40 (см²)
Ответ: ≈ 40 см²