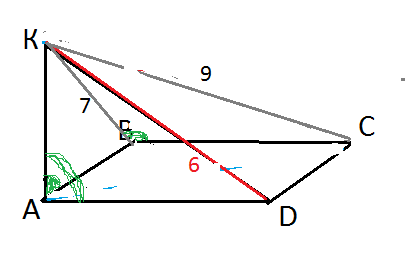
В основании прямоугольник. В прямоугольнике все углы прямые.
AB⊥BC
АВ- проецкия наклонной КВ.По теореме о трёх перпендикулярах КВ⊥ВС.
Значит треугольник КВС - прямоугольный
По теореме Пифагора
ВС²=КС²-КВ²=9²-7²=32
ВС=√32=4√2
Противоположные стороны прямоугольника равны, значит АD=BC=4√2
Треугольник АКD - прямоугольный. ( АК⊥ плоскости АВСD, а значит перпендикуляр любой прямой , лежащей в этой плоскости)
По теореме Пифагора
AK² = KD²- AD²=6²-(4√2)²=36-32=4
AK=2
Расстоянием между скрещивающимися прямыми
АК и СD будет расстояние между плоскостями АКВ и плоскостью, параллельной этой плоскости и проходящей через CD.
Это расстояние равно AD
ответ. АК =2 см, АD= 4√2 cv