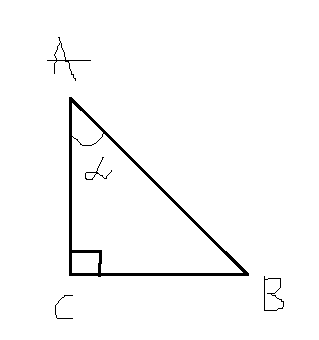
Рассмотрим с помощью прямоугольного треуглольника
sin A это соотношение противолежащего катета на гипотенузу
Sin A = BC/AB = (2√2)/3
Стороны: BC = 2√2 (см), AB = 3 (см)
За т. Пифагора определяем АС
AB² = AC² + BC²

cos A это соотношение прилежащего катета на гипотенузу, тоесть
cos A = AC/AB=1/3
Так как cos A = 1/3 домножим на 3
Cos A = 1/3 |×3
3Cos A = 1
Ответ: 1.