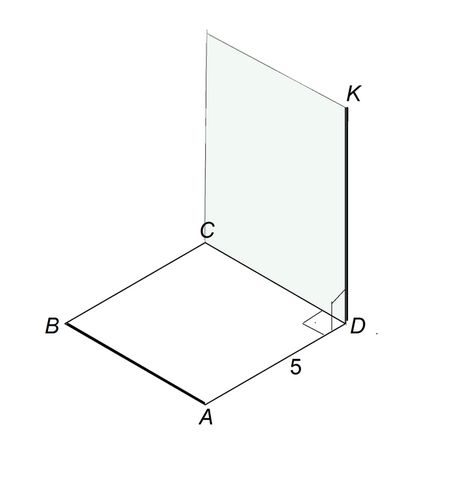
Казалось бы, очевидно, что расстоянием между АВ и КD является АD=5.
Но это утверждение следует доказать.
------
1)Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.
КD пересекает плоскость квадрата АВСD в точке, не лежащей на прямой АВ.
КD и АВ - скрещивающиеся.
2)Прямые КD и СD пересекаются.
Следовательно, через них можно провести плоскость, притом только одну.
АВ и СD параллельны как противоположные стороны квадрата.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
⇒Прямая АВ параллельна плоскости КDС, содержащей КD
Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.
Расстояние между АВ и КD - это расстояние между АВ и плоскостью КDС
Расстояние между параллельными прямой и плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.
Расстояние между АВ и плоскостью КDС - это длина перпендикулярного АВ и КD отрезка АДD.
Расстояние между прямыми АВ и КD равно 5 см.