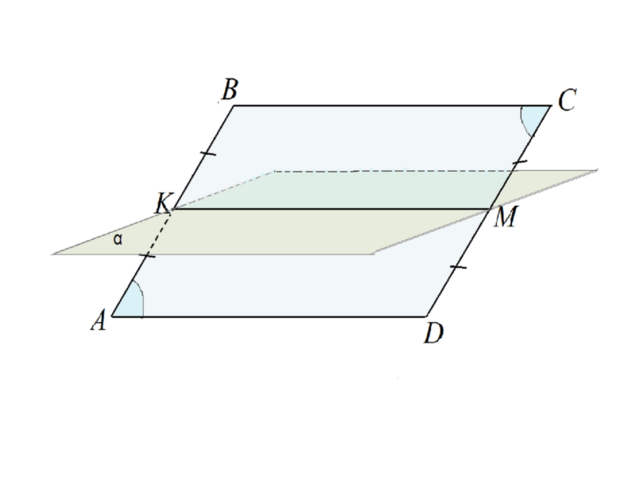
Плоскость параллеограмма АВСD пересекается с плоскостью альфа по прямой, соединяющей середины сторон АВ и СD.
По условию ВК=МС; ВК|| МС.
Если две стороны четырехугольника равны и параллельны, этот четырехугольник - параллелограмм.
⇒КМ || ВС
Через две параллельный прямые можно провести плоскость, притом только одну.
Так как ВС не лежит в плоскости альфа, то АD, как сторона параллелограмма, равная и параллельная ВС и лежащая в плоскости АВСD, тоже не лежит в плоскости альфа, в противном случае через ВС и АD можно было бы провести плоскость, отличную от плоскости АВСD.
ВС || КМ ⇒ КМ || АD.
Если прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в плоскости, то она параллельна этой плоскости.
AD параллельна КМ ⇒ параллельна плоскости α, что и требовалось доказать.