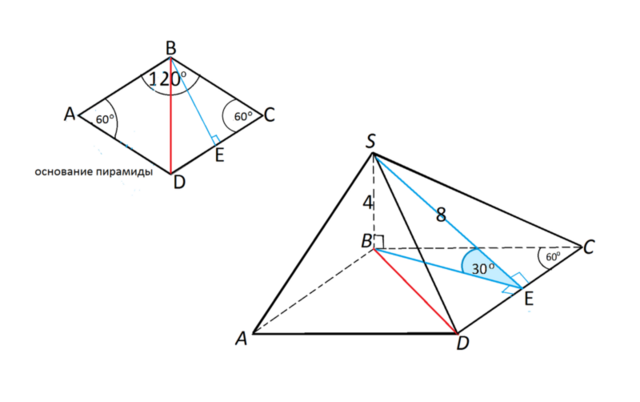
Основанием пирамиды является ромб, тупой угол которого равен
120 °. Две боковые грани пирамиды, содержащие стороны этого
угла, перпендикулярны к плоскости основания, а две другие
боковые грани наклонены к плоскости основания под углом 30 °. Найдите площадь боковой поверхности пирамиды (в см²), если ее высота равна 4 см.
-----------
Сделаем рисунок пирамиды и её основания.
Сумма углов параллелограмма при одной стороне равна 180°, ⇒
острый угол ромба равен 180°-120°=
60°, ⇒
треугольники АВD и ВDС- равносторонние и равны между собой.
Площадь боковой поверхности пирамиды - сумма площадей всех ее граней, найденных для каждой по формуле
S=ah:2
Грани SВС и SВA - равные прямоугольные треугольники.
Их высота - общая с высотой пирамиды и равна 4 см
Плоскости двух других граней SDС и SDА ( они
тоже равны между
собой по 2-м равным сторонам и одной общей) составляют с
плоскостью основания угол 30°.
Известно, что
угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
В равнобедренных треугольниках с общим основанием перпендикуляры из вершин, противолежащих основанию, пересекаются на нем в одной точке:
SE
⊥DC
BE
⊥DC
Угол SEВ=30°
Так как высота пирамиды перпендикулярна ее основанию,
⊿ SВE -
прямоугольный, катет SВ противолежит углу 30°, и
SE ( она - гипотенуза ⊿ SBE и высота треугольника DSE ) равна
2SВ=8 см
Высоты граней известны, найдем сторону ромба.
Высота ромба
ВЕ=SE·соs(30°)=
4√3 см
ВС=ВЕ
:sin(60°)=(4√3)
:{(√3)
:2}=
8 см
Можно обойтись без этих вычислений:
В прямоугольных треугольниках SBE и CBE равны углы и катет ВЕ.
Если острый угол и катет одного прямоугольного треугольника равны острому углу и катету другого - эти треугольники равны.
Найдены основания и высоты граней
, следовательно
:
S бок=2S⊿SАВ+2S△SDС
S⊿SАВ=ВS
·AВ
:2=4*8
:2=16 см²
S△SDС=SE
·CD
:2=8
·8
:2=32 см²
S бок=2
·16 + 2
·32=
96 см²
-------------
[email protected]