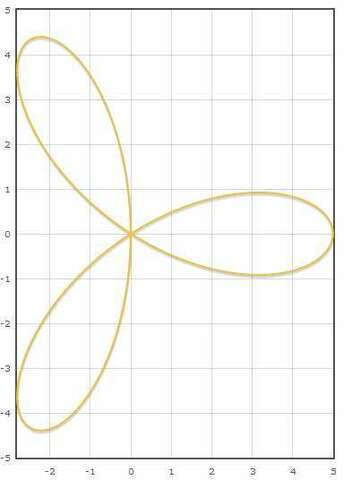
r = a cos3fi
1. график в полярных координатах представляет собой трехлепестковую розу.2. Найдем область определения функции на отрезке от 0 до 2пДолжно выполняться неравенствоcos3fi >=0На отрезке от 0 до 2п данное условие выполняется когда
0 + 2пк <= 3fi < п/2 + 2пк и 3п/2+ 2пк <= 3fi <= 2п+ 2пк (1)<br>Тогда получаем, что Fi должен удовлетворять условиям 0 <= fi <= п/6 и п/2<= fi <= 2п/3, 2п/3<= fi < п/6 +2п/3, п/2 + 2п/3 <= fi <= 4п/34п/3 <= fi <= п/6 +4п/3п/2 + 4п/3 <= fi <= 2п<br>или
0 <= fi <= п/6,п/2<= fi < п/6 +2п/3, п/2 + 2п/3 <= fi <= п/6 +4п/3,п/2 + 4п/3 <= fi <= 2п<br>3. Лепестки равны друг другу, поэтому воспользуемся формулой вычисления площади фигуры в полярных координатах
S = 1/2* интеграл от альфа до бетта r2(fi)dfi
площадь нашей фигуры, состоящей из трех лепестков, будет равна трем площадям первого лепестка.
Так как функция периодическая, то заменим последний отрезок из области определения п/2 + 4п/3 <= fi <= 2п на более удобный, когда к = -1 в формуле (1)<br>Тогда -п/6 <= fi <= 0<br>тогда в нашем случае альфа равна -п/6, а бетта равна п/6.
S = 3/2 * интеграл от -п/6 до п/6 а2 (cos 3fi)2 dfi =
3/2 *а2* интеграл от -п/6 до п/6 ( 1 + cos6fi)/2 dfi =
3/4 *а2* (fi + (sin6fi)/6) от -п/6 до п/6 = 3/4 *а2*( п/6 - (-п/6) = 3/4а2*п/3 = па2/4 так как sin п и sin -п равны нулю.