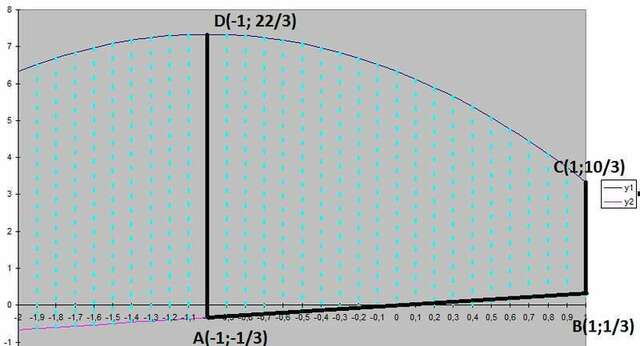
Вычислим координаты вершин фигуры. А( -1;-1/3), В(1;1/3), С( 1; 10/3) и D( -1 ; 22/3)
y1 = 22/3 - (x + 1)2
y2 = x/3
Площадь криволинейной трапеции под графиком функции у1 вычисляется по формуле
интеграл от -1 до 1 ( 22/3 - (x + 1) 2) = 22/3x -(x+1)3/3 от -1 до 1 =
22/3 - 8/3 - ( -22/3 ) = 44/3 - 8/3 = 36/3 = 12
Криволинейная трапеция ограничена графиком функции y1 и прямыми х =1, х = -1, y = 0;
Для вычисления площади искомой фигуры нужно вычесть площадь треугольника c вершинами (0;0), ( 1;1/3) (1;0) и прибавить площать треугольника с вершинами (-1;-1/3) ( -1;0) и (0;0). Площади треугольников равны , поэтому площадь искомой фигуры равна 12