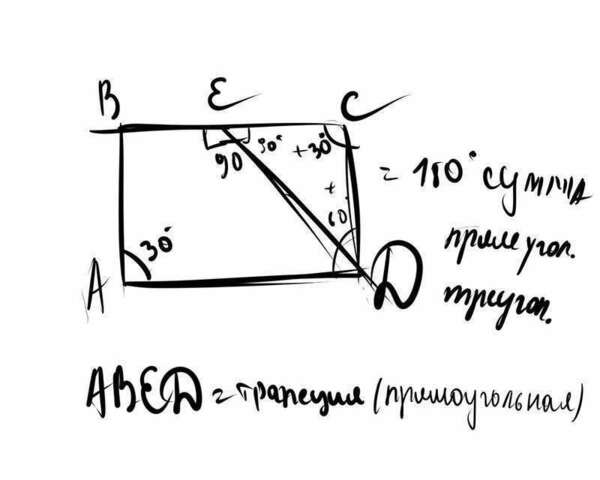
Так смотри. Начертим сначала четырех. ABCD. Из угла D проведем прямую к точке Е. Так смотрим, получается здесь есть и треугольник (прямоугольный причем) и прямоугольная трапеция. Сейчас докажем.
Док-во:
Расс-им четырехугол. ABCD и треугольник CDE. Из дано сказано что: угол А=30 градусов и AB=CD, BC=AD, противоположные углы и стороны в паралеллограмме ( или в четырехугольнике, это правила паралелограма имеют свойство быть в правилах четырехугольника, это одно и тоже) равны значит угол С= 30.
Итак из дано сказано что CDE=60, значит 60+30=90-это угол E, он прямой. Разобрали треугольник DEC. Разберем трапецию ABED, известно что угол А= 30 градусов, но если угол Е в треугольнике равен 90, то и угол Е в трапеции будет равен 90, а в прямоугольной трапеции угол равен 90 градусов. Сумма углов трапеции=180 если надо конечно найти другие углы