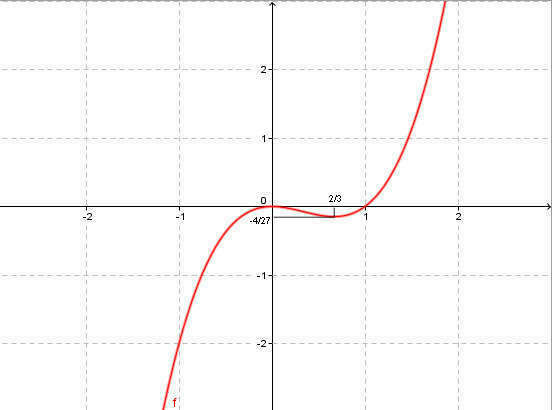
F(x)=x³-x²
Поведение на бесконечности:
при х⇒-∞ y⇒-∞
при х⇒∞ y⇒∞
Точки пересечения с осью х:
у=0
x³-x²=0
x²(x-1)=0
Произведение равно 0, когда хотя бы один из множителей равен 0
x₁=0
x₂-1=0
x₂=1
(0;0) (1;0)
Точки пересечения с осью у:
х=0
у=0
(0;0)
Находим экстремуму функции. Производную приравниваем нулю
y'=3x²-2x
3x²-2x=0
x(3x-2)=0
x₁=0
3x₂-2=0
x₂=2/3
Отмечаем найденные точки на числовой прямой и находим знак производной в интервалах
+ - +
-----------------₀----------------₀------------------->
0 2/3
Производна меняет знак с плюса на минус в точке х=0. Значит, это точка максимума.
f(0)=0
Производна меняет знак с минуса на плюс в точке х=2/3. Значит, это точка минимума.
f(2/3)=(2/3)³-(2/3)²=8/27-4/9=(8-4*3)/27=-4/27
Ищем наклонные асимптоты (если вы их ищите)

Это означает, что наклонных асимптот нет.
Строим график