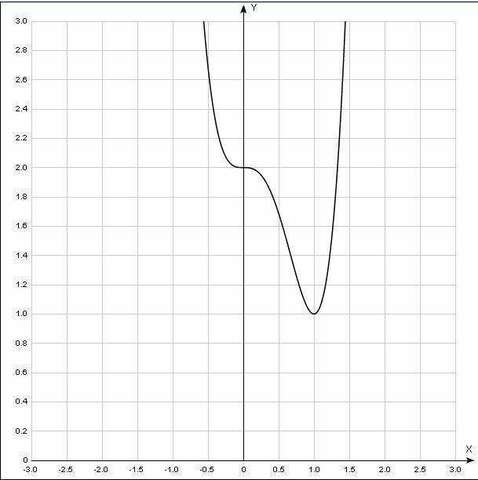
При x∈(1; +бесконечность) функция возрастает (т.к. производная положительная)
При x∈(-бесконечность; 0)u(0;1) функция убывает (т.к. производная отрицательная)
x = 0 - точка перегиба
x = 1 - локальный минимум
P.S. График функции в подтверждение решения
Ответ: нет максимума функции