#2

#3

#4
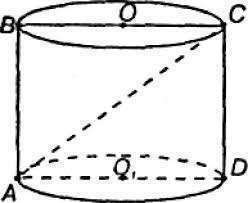
Дано: цилиндр, ABCD - осевое сечение, AB=AD, BD=3√2 см.
Найти: Sполн.пов.
Решение:
Из прямоугольного треугольника АВС по теореме Пифагора BD^2 = 2AB^2, откуда AB = BD/√2 = 3√2/√2 = 3 (см)
Поэтому высота цилиндра АВ=3 см, радиус цилиндра ОА = 1,5 (см)
Площадь боковой поверхности = 2 * pi * 1,5 * 3 = 9 * pi (см)
Площадь основания = pi * 1,5^2 = 2,25 * pi (см)
Площадь полной поверхности = 9 * pi + 2 * 2,25 * pi = 13,5 * pi (см^2)
Ответ: 13,5 * pi (см^2)