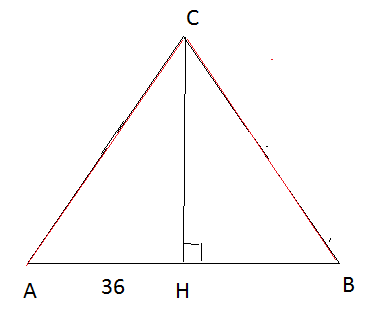
1) Высота СН в равнобедренном треугольнике является и медианой.
Поэтому АН = 36 ( см. рис.1)
cos∠ CAH= 12√1/13
По определению косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
(12√1)/13= АН : AС ⇒ (12√1)· АС= 13 ·АН,
(12√1)· АС= 13· 36,
(√1)·AС=13·3
AС=39
По теореме Пифагора
СН²=АС²-АН²=39²-36²=(39-36)(39+36)=3·75=9·25=(15)²
СН=15
2) По определению тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
tg ∠ A= ВС : АС ⇒ АС= ВС : tg ∠ A=15 : (3√10/20)=100/(√10)
По теореме Пифагора AB² = BC² + AC²=15² + (100/√10)²=225+1000=1225=35²
AB=35
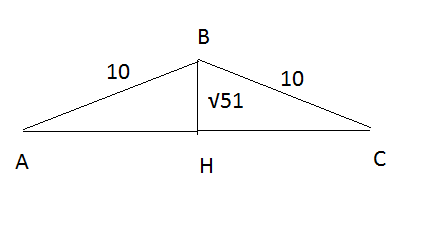
3) Cм. рис. 2
Рассмотрим прямоугольный треугольник АВН.
sin ∠ BAH= BH : AB= (√51/10), значит sin ∠ АВН= sin (90°- ∠ BAH)= сos
∠ BAH=√(1-sin²∠ BAH)=√(1-(√51/10)²)=√(1-51/100)=√49/100=7/10
Итак,
sin ∠ АВН= 7/10, тогда сos ∠ АВН= (√51)/10
sin ABC= 2·sin ∠ АВН· сos ∠ АВН= 2·( 7/10)·(√51)/10=(14√51)/(100)
4) Из треугольника АСН tg∠ А= СН : АН ⇒ СН=3,5
Известно, что высота прямоугольного треугольника есть среднее пропорциональное между отрезками гипотенузы ( или это можно получить из подобия треугольников АСН и АВС):
СН²=АН·ВН ⇒ 3,5² = 7·ВН ⇒
ВН=3,5/2=1,75
5) См. рис. 2. ВН- высота равнобедренного треугольника является и медианой.
sin ∠ А=(√51)/10
сos ∠ А=√1- ((√51)/10)²=√49/100=7/10
По определению косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
сos ∠ А= АН : АВ ⇒ АН=АВ·сos ∠ А=10,5 ·7/10=73,5/10=7,35
АС= АН+НС=7,35+7,35=14,7