При каких значениях х имеет смысл выражение log по основанию 1/3 (x^3 + x^2 - 2x)

Question

При каких значениях х имеет смысл выражение

log по основанию 1/3 (x^3 + x^2 - 2x)

Answer 1

Выражение имеет смысл,когда под логарифмом стоит положительная величина.
Тогда

0 \\ x(x^2+x-2)>0 \\ x^2+x-2=0 \\ x1+x2=-1 \\ x1*x2=-2 \\ \\ x1=-2 \\ x2=1 \\ \\ x(x+2)(x-1)>0 \\ x=0 \\ x=-2 \\ x=1" alt="x^3+x^2-2x>0 \\ x(x^2+x-2)>0 \\ x^2+x-2=0 \\ x1+x2=-1 \\ x1*x2=-2 \\ \\ x1=-2 \\ x2=1 \\ \\ x(x+2)(x-1)>0 \\ x=0 \\ x=-2 \\ x=1" align="absmiddle" class="latex-formula">

Далее методом интервалов
  _        +        _         +
......-2.///////.0.......1./////////

Answer 2

выражение имеет смысл, если выражение под логарифмом положительно, т.е
0" alt="x^3 + x^2 - 2x>0" align="absmiddle" class="latex-formula">
0" alt="x(x^2+x-2)>0" align="absmiddle" class="latex-formula">
рассмотрим выражение в скобке (разложим его на множители)

тогда

возвращаемся к неравенству
0\\x(x+2)(x-1)>0" alt="x(x^2+x-2)>0\\x(x+2)(x-1)>0" align="absmiddle" class="latex-formula">
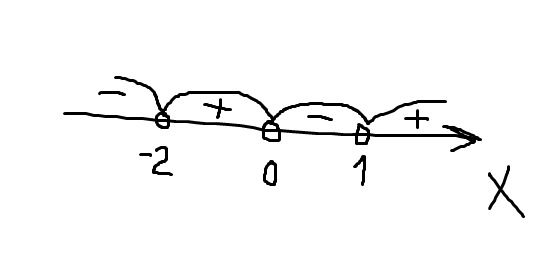
методом интервалов получаем, что

---