Помогите пожалуйста.диагональ прямоугольного параллелепипеда равна 7 см,а диагонали двух...

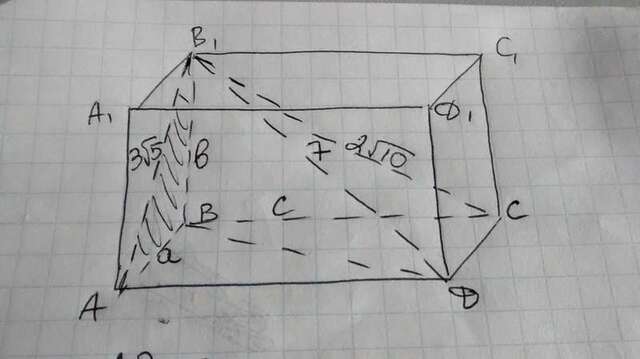
$\left \{ {{b^2+a^2+40-b^2=49} \atop {a^2+b^2=45}} \right. \\ a^2=49-40 \\ a^2=9 \\ a=3 - AB$ Пусть $AB =a,BC=b,BB_=c. \\ BB_1^2+BA^2=AB_1^2 \\ b^2+a^2=( 3\sqrt{5} )^2 \\ \\ AB^2+AD^2=BD^2 \\ a^2+c^2=BD^2 \\ BB_1^2+BD^2=B_1D^2 \\ b^2+a^2+c^2=(7)^2 \\ \\ BB_1^2+BC^2=B_1C^2 \\ b^2+c^2=(2 \sqrt{10} )^2$

Имеем систему их трех уравнений с тремя неизвестными:
$\left \{ {{b^2+a^2+c^2=49}; \atop {a^2+b^2=45} ; \atop {c^2+b^2=40}} \righteft.$

Выразим с третьего ур-ния $c^{2} =40- b^{2}$ и подставим в первое ур-ние.
Имеем систему 2х ур-ний с 2мя неизвестными, из которого находим $a$ :
$\left \{ {{b^2+a^2+40-b^2=49} \atop {a^2+b^2=45}} \right. \\ a^2=49-40 \\ a^2=9 \\ a=3$
$a$ - длина $AB$

Из ур-ния $a^2+b^2=45$ найдем $b$ :
$b^2=45-9 \\ b^2=36 \\ b=6$ - длина $BB_1$ .

Из ур-ния $c^2+b^2=40$ найдем $c$ :
$c^2=40-36 \\ c^2=4 \\ c=2$ - длина $BC$ .

Площадь полной поверхности параллелепипеда:
$S = P_{ABCD}*AA_1=(3*2+2*2)*6=10*6=60$ см^2.