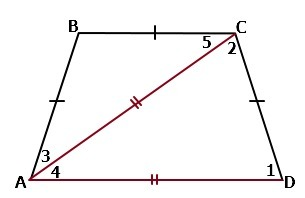
Дано: ABCD - трапеция, BC║AD, AB=BC=CD, AC -
диагональ, AC=AD
Найти: ∠A, ∠B, ∠C, ∠D
Решение:
Обозначения: ∠1 = ∠CDA, ∠2 = ACD, ∠3 = ∠BAC, ∠4 = CAD, ∠5 = ∠BCA
1. Рассмотрим ΔACD: AC=AD (по усл)⇒ ΔACD - равнобедренный ⇒ ∠2 = ∠1
2. Рассмотрим ΔABC: AB=BC (по усл)⇒ ΔABC -
равнобедренный ⇒ ∠3 = ∠5
3. Рассмотрим ∠5 и ∠4, т.к. BC║AD (по усл), то ∠5 и ∠4 внутренние накрест лежащие углы ⇒ ∠5 = ∠4 и, исходя из предыдущего пункта 2, получаем: ∠3 = ∠5 = ∠4
4. Сумма углов
трапеции, прилежащих к боковой стороне, равна 180°, т.е. ∠C + ∠D = 180° ⇒ ∠5 + ∠2 + ∠1 = 180°, но из пункта 1: ∠2 = ∠1, поэтому запишем так: ∠5 + 2 *∠2 = 180°
5. С другой стороны, т.к. ABCD - равнобедренная, то ∠A = ∠D, т.е. ∠3 + ∠4 = ∠1, но, исходя из пункта 1: ∠2 = ∠1, получаем: ∠3 + ∠4 = ∠2. А, исходя из пункта 3: ∠3 = ∠5 = ∠4 ⇒ 2 * ∠5 = ∠2
6. Подставим полученное в пункте 5 значение ∠2 в выражение из пункта 4:
∠5 + 2 *∠2 = 180°
∠5 + 2 *2 * ∠5 = 180°
5 * ∠5 = 180° ⇒ ∠5 = 180°/5 = 36°
7. Исходя из пункта 3: ∠3 = ∠5 = ∠4 ⇒ ∠3 = ∠5 = ∠4 = 36°, т.е. ∠A = ∠D = ∠3 + ∠4 = 36° + 36° = 72°
8. ∠B = ∠C = ∠5 + ∠2 = 36°+72° = 108°
Ответ: ∠A = ∠D = 72°, ∠B = ∠C = 108°