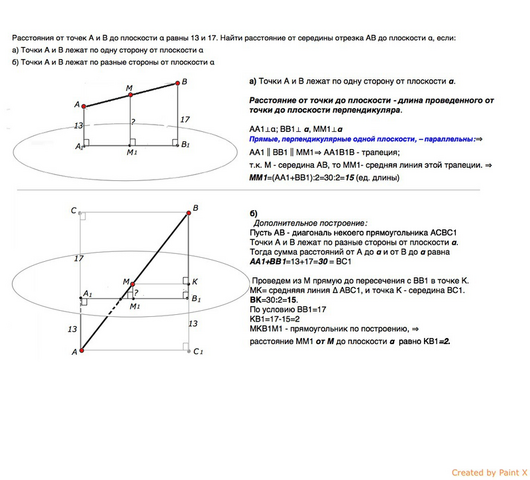
А) Точки А и В лежат по одну сторону от плоскости α.
Расстояние от точки до плоскости - длина проведенного от точки до плоскости перпендикуляра.
АА1⊥α; ВВ1⊥ α, ММ1⊥α
Прямые, перпендикулярные одной плоскости, параллельны. ⇒
АА1║ВВ1║ММ1⇒ АА1В1В - трапеция, а, т.к. М - середина АВ, –
ММ1- средняя линия этой трапеции. ⇒
ММ1=(АА1+ВВ1):2=30:2=15 (ед. длины)
б)
Точки А и В лежат по разные стороны от плоскости α.
Тогда сумма расстояний от А до α и от В до α равна
АА1+ВВ1=13+17=30
Пусть АВ - диагональ некоего прямоугольника АСВС1
Проведем из М прямую параллельно А1В1 до пересечения с ВВ1 в точке К. Угол МКВ1- прямой.
МК= средняяя линия ∆ АВС1, и точка К - середина ВС1.
ВК=30:2=15.По условию ВВ1=17
КВ1=17-15=2
МКВ1М1 - прямоугольник по построению, ⇒ расстояние ММ1 от М до плоскости равно КВ1=2(ед. длины)