То, что значение интеграла будет <0, можно было обнаружить и не вычисляя первообразную.<br>График подынтегральной функции у=22х-22 - прямая, пересекающая ось ох в точке х=1
и на [0;1] прямая расположена ниже оси ох.
Поэтому по свойству определенного интеграла, если функция f(x) ≥ 0 на отрезке [a; b] и a
0" alt="2) (f(x)-g(x))`=(22x-22)`=22, \\ \int\limits^1_0 {(f(x)-g(x))`(2f(x)-g(x))} \, dx = \int\limits^1_0 {22\cdot(2(29x+7)-(7x+29))} \, dx= \\ =\int\limits^1_0 {22\cdot(58x+14-7x-29)} \, dx= \int\limits^1_0 {22\cdot(51x-15)} \, dx>0" align="absmiddle" class="latex-formula">
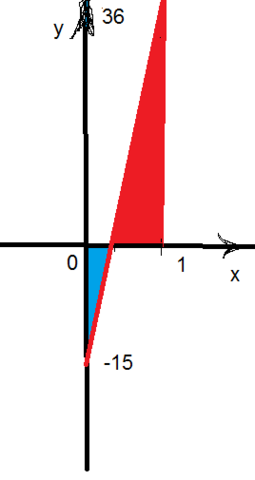
Так как графиком подынтегральной функции у=51х-15 является прямая, пересекающая ось ох в точке х=15/51=5/17
на [0; 5/17] прямая расположена ниже оси ох и значение интеграла отрицательно, а на [5/17;1] прямая расположена выше оси ох и значение интеграла положительно.
Но та часть, которая расположена на [5/17;1] по величине больше, см рисунок
Красным цветом положительное значение интеграла, синим отрицательное. Красного больше
Графиком подынтегральной функции у=(22х-22)(138х+6) является парабола, пересекающая ось ох в точках
х=-6/138 и х=1
На [0;1] расположена ниже оси ох.
Поэтому по свойству определенного интеграла, если функция f(x) ≤0 на отрезке [a; b] и a
