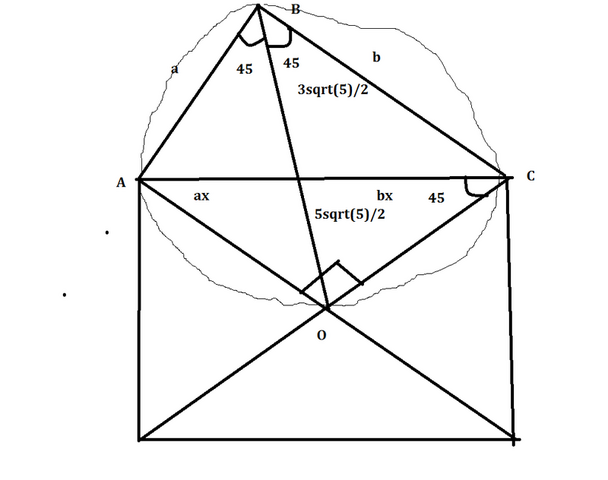
Сумма углов O+C=180 градусов (диагонали квадрата перпендикулярны)
То около 4 угольника ABCO можно описать окружность,таким образом углы OCA=ABO,как опирающиеся на 1 дугу.
OCA=45 тк диагональ квадрата делит его углы по 45.
Таким образом BO-бессектриса угла C. По свойству бессектрисы даны доли отношений.(ax ,bx)
А по свойству хорд получим: 3sqrt(5)/2*5sqrt(5)/2=ax*bx
x^2=75/4ab
Площадь треугольника ABC равна сумме площадей треугольников бьющихся бессектрисой.
1/2ab=1/2a*3sqrt(5)/2 *sin45+1/2b*3sqrt(5)/2 *b*sin45
Откуда ab=3sqrt(10)/4 *(a+b)
Ну и наконец по теореме пифагора:
a^2+b^2=(ax+bx)^2=(a+b)^2*x^2=(a+b)^2*75/4ab
то есть нужно решить систему:
ab=3sqrt(10)/4*(a+b)
(a^2+b^2)*4ab=75(a+b)^2
Ну конечно эту систему можно решить но я этого делать явно не хочу.
Существует такая теорема -теорема Птолимея,которая гласит что если 4 угольник вписан в окружность,то сумма произведений противолежащих сторон равна произведению его диагоналей.
То тк полудиагональ равна c*sqrt(2)/2
То выходит что: a*c*sqrt(2)/2 +b*c*sqrt(2)/2=c*4sqrt(5)
a+b=4sqrt(10)
Ну и еще 1 уравнение
ab=3sqrt(10)/4 *(a+b)
ab=3sqrt(10)*4sqrt(10)/4=30
a+b=4sqrt(10)
По теореме обратной теореме виета a и b корни уравнения
x^2-4sqrt(10)*x+30=0
D=160-120=40=(2sqrt(10))^2
x=(4sqrt(10)+-2sqrt(10))/2
a=3sqrt(10)
b=sqrt(10)
c=sqrt(90+10)=10!!!
Может в условии нужно искать гипотенузу а не стороны треугольника :)
Ответ:3sqrt(10),sqrt(10),10