1) Докажем по определению:
"Параллелограммом называется четырехугольник у которого противоположные стороны попарно параллельны".
по аксиоме любые три точки всегда лежат в одной плоскости.
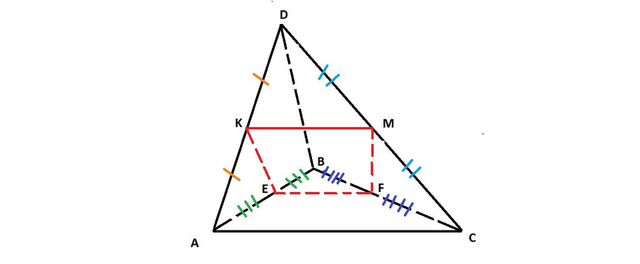
Значит четвертая точка не лежит в данной плоскости. Если все 4 точки соединить между собой, то получится треугольная пирамида (тетраэдр)
рассмотрим ΔАВС:
Если Е и F - середины сторон АВ и ВС, то EF - средняя линия треугольника (по определению), следовательно EF || AC.
аналогично для других треугольников:
KM - средняя линия треугольника ADC значит КM || AC
Если EF || AC и КM || AC, то EF || KM (закон транзитивности)
EK - средняя линия треугольника ADB, значит EK || BD
MF- средняя линия треугольника CDB, значит MF || BD
Если EK || BD и MF || BD, то EK || MF
Итак, EF || KM и EK || MF, следовательно EFKM-параллелограмм (по определению) - ч.т.д.
2) средняя линия треугольника равна половине основания
KE=MF=BD/2=8/2=4 см
KM=EF=AC/2=6/2=3 см
Периметр (Р) - сумма длин всех сторон
KE+MF+KM+EF=4+4+3+3=14 см
Отв: 14 см