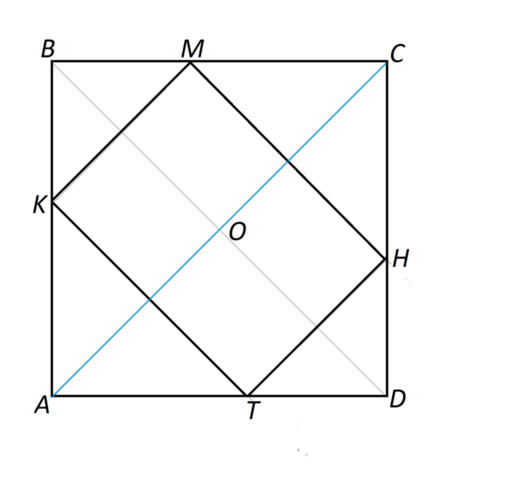
В квадрат вписан прямоугольник так, что на каждой стороне квадрата лежит вершина прямоугольника, а его стороны параллельны диагоналям квадрата. Найти стороны прямоугольника, если одна из них на 6 см больше другой, а диагональ квадрата равна 30 см
Сделаем рисунок.
Треугольники ВМК, АКТ, МСН и НDT - равнобедренные прямоугольные.
ОА=АС:2=15 см
Пусть ВК=х
Тогда АК=АВ-х
По известному свойству гипотенузы равнобедренного прямоугольного треугольника
АВ=15√2
АК=15√2 -х
КМ=х√2
КТ=(15√2 -х )*√2=
30-х√2
По условию КТ-КМ=6 см
30-х√2 -х√2=6
24=2х√2
х=24:2√2=
12:√2
Умножим числитель и знаменатель на √2, чтобы избавиться от дроби:
х=12:√2=(12*√2):√2*√2х=
6√2
КМ=6√2*√2=
12 см
КТ=30-х√2=30-12=18 см
КТ-КМ=18-12=6 см