Cистема неравенств не имеет решений. Первое неравенство неверно. Не выполняется ни при каком х, слева 0 при любом х, 0<-9 - неверно<br>

\frac{5x}{2}- \frac{7}{8} } \atop { \frac{2x+1}{4}<5- \frac{1-2x}{3} }} \right. " alt="2) \left \{ {{ \frac{x}{2}- \frac{7}{4}> \frac{5x}{2}- \frac{7}{8} } \atop { \frac{2x+1}{4}<5- \frac{1-2x}{3} }} \right. " align="absmiddle" class="latex-formula">
Умножим первое неравенство на 8, второе на 12

20x-7} \atop {3(2x+1)<5-4(1-2x)}} \right. \\ \left \{ {{-16x>7} \atop {6x+3<5-4+8x}} \right. \\ \left \{ {{x<- \frac{7}{16} } \atop {-2x<-2}} \right. \\ \left \{ {{x<- \frac{7}{16} } \atop {x>1}} \right. " alt=" \left \{ {{4x-14>20x-7} \atop {3(2x+1)<5-4(1-2x)}} \right. \\ \left \{ {{-16x>7} \atop {6x+3<5-4+8x}} \right. \\ \left \{ {{x<- \frac{7}{16} } \atop {-2x<-2}} \right. \\ \left \{ {{x<- \frac{7}{16} } \atop {x>1}} \right. " align="absmiddle" class="latex-formula">
Система не имеет решений, множества решений первого и второго неравенств не пересекаются.

3-5x} \atop {3x+2>3-4x}}\atop {5x-3<2x+5} } \right. \\ \left \{ {{2x+5x>3+1} \atop {3x+4x>3-2}}\atop {5x-2x<3+5} } \right. \\ \left \{ {{7x>4} \atop {7x>1}}\atop {3x<8} } \right. " alt="3) \left \{ {{2x-1>3-5x} \atop {3x+2>3-4x}}\atop {5x-3<2x+5} } \right. \\ \left \{ {{2x+5x>3+1} \atop {3x+4x>3-2}}\atop {5x-2x<3+5} } \right. \\ \left \{ {{7x>4} \atop {7x>1}}\atop {3x<8} } \right. " align="absmiddle" class="latex-formula">
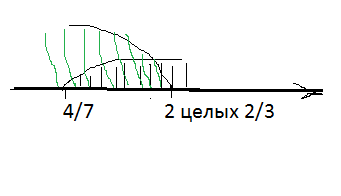
Ответ. 4/7см. рисунок