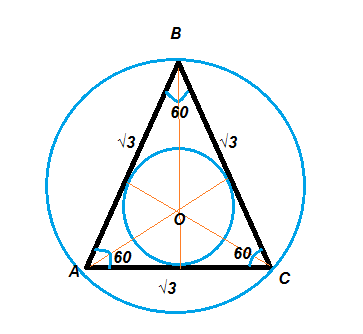
Дан треугольник АВС. Точка О - центр описанной окружности. АВ = ВС =√3.
Так как угол 60 градусов то другие также по 60 градусов, следовательно треугольник равносторонний: AB = BC = AD = √3
Радиус описанной окружности около равностороннего треугольника:

Ответ: R = 1