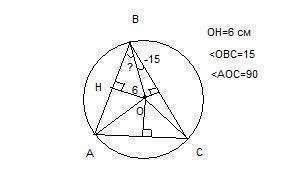
Центральный угол АОС опирается на дугу АС, значит градусная мера дуги АС равна 90°. Треугольник ВОС - равнобедренный, т.к. ОВ=ОС=r. Значит, углы при его основании ВС равны между собой:
Зная сумму углов треугольника, находим угол ВОС:
Угол ВОС - центральный и опирается на дугу ВС, значит ВС=150°
Дуга АВ равна 360 - АС - ВС = 360-90-150=120°
Центральный угол АОВ опирается на дугу АВ, значит
Треугольник АОВ - равнобедренный, т.к. ОА=ОВ=r. Значит, углы при его основании АВ равны между собой:
Рассмотрим прямоугольный треугольник ОНВ. Катет ОН, лежащий против угла в 30°, равен половине гипотенузы ОВ. Значит
ОВ=2*ОН=2*6=12 см
r=OB=12 см