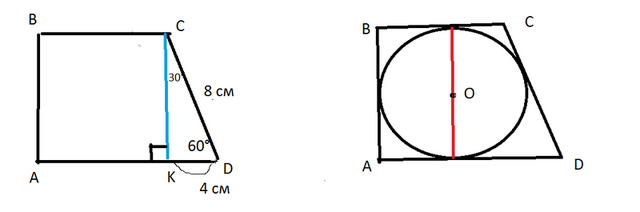
В прямоугольной трапеции, один из углов равен 60
градусов, большая боковая сторона равна 8 см. Найдите основания трапеции
и радиус вписанный в нее окружности.=========================================================================
См. рисунок 1.
Проведем высоту СК.
В прямоугольном треугольнике CKD катет КD равен половине гипотенузы, так как лежит против угла в 30°
KD = 4 см.
Тогда по теореме Пифагора СК²=СD² - KD²= 8²-4²=64-16=48
CK=4√3 см.
По свойству четырехугольника, описанного около окужности, суммы противоположных сторон равны
АВ + CD = ВC + AD
Значит ВС + AD = 4√3 + 8
Но так как BC = AK и AD = АК + KD = ВС + KD,
то ВС + ВС + 4 = 4 √3 + 8 ⇒ 2 ВС = 4√3 + 4 ⇒ ВС = 2√3 + 2
AD = BC + KD = 2√3 + 2 + 4 = 2 √3 + 6
r = CK/2 = 4√3/2 = 2√3
Ответ. верхнее основание 2√3 + 2, нижнее основание 2 √3 + 6, радиус вписанной окружности
2√3