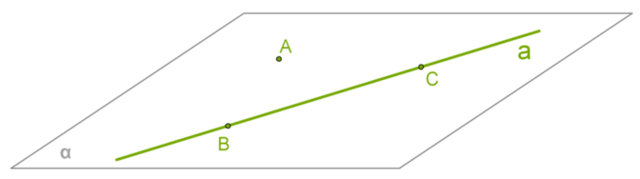
1. Через прямую и не лежащую на ней точку можно провести плоскость, притом только одну. Доказательство:
1) Рассмотрим прямую a и точку A, которая не находится на этой прямой.
2) На прямой a выберем точки B и C.
3) Так как все 3 точки не находятся на одной прямой, из второй аксиомы следует, что через точки A, B, C и можно провести одну единственную плоскостьα.
4) Точки прямой a, B и C, лежат на плоскостиα, поэтому из третьей аксиомы следует, что плоскость проходит через прямую a и, конечно, через точку A.