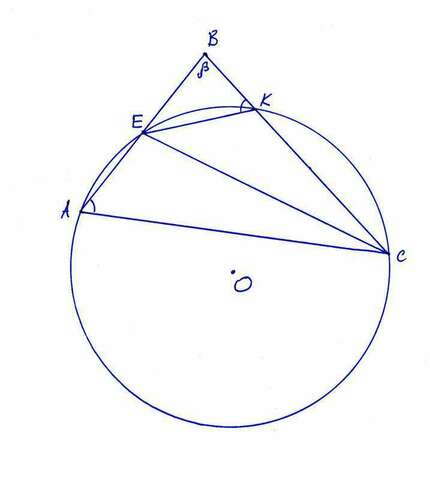
Пусть точка E - середина AB.
Вокруг четырехугольника AEKC
можно описать окружность.
Поэтому сумма углов EKC и BAC равна 180°, что
означает, что угол EKB = угол BAC, то есть треугольники ABC и BEK подобны (у
них все углы равны).
Из этого подобия следует BK/BA = BE/BC, или, если положить
AB = c, AC = b, BC = a, то
(a/4)/c = (c/2)/a; a = c√2;
коэффициент подобия треугольников ABC и BEK равен √2/4;
это
легко получается из условия.
Далее, пусть угол ABC = β; и еще надо обозначить CE = m;
(это медиана треугольника ABC к стороне AB).
Из условия известно, что радиус окружности, описанной вокруг
треугольника AEC, равен 5.
Кроме того, известно, что площадь ACE равна половине площади
ABC, поскольку CE - медиана.
Как уже было найдено, если AB = c, то AE = c/2; BC = c√2;
откуда
Sabc = BA*BC*sin(β)/2 = (c^2)*√2*sin(β)/2;
Seac = Sabc/2 =
(c^2)*√2*sin(β)/4;
По теореме косинусов для треугольника ABC
(AC)^2 = b^2 = c^2 + (c√2)^2 - 2*c*(c√2)*cos(β) = (c^2)*(3 -
2√2*cos(β));
по теореме косинусов для треугольника EBC
(EC)^2 = m^2 = (c/2)^2 + (c√2)^2 - 2*(c/2)*(c√2)*cos(β) =
(c^2)*(9/4 - √2*cos(β));
Далее, используя известную формулу (R = abc/4S) для радиуса
описанной окружности для треугольника AEC, легко получить
5 = AE*AC*EC/(4*Saec) =
(c/2)*(c√(3 - 2√2*cos(β)))*(c√(9/4 -
√2*cos(β))/((c^2)*√2*sin(β));
или
5 = с*(√(3 - 2√2*cos(β)))*(√(9/4 - √2*cos(β))/(2√2*sin(β));
Никаких дополнительных условий в задаче нет, то есть угол ABC = β; может принимать любые значения из области определения полученной функции.
Кроме того, подобие треугольников ABC и KBE при любом значении β ВСЁ РАВНО означает, что вокруг четырехугольника AEKC можно описать окружность Правда, радиус этой окружности зависит от угла ABC = β. Но из последнего соотношения видно, что этот радиус пропорционален стороне AB = c. Что означает, что из условия задачи И НЕЛЬЗЯ определить, чему равен β.
Поэтому из этого соотношения следует два вывода
1) условие задачи СКОРЕЕ ВСЕГО не полное, точнее - в задаче есть неопределенный параметр.
2) последнее соотношение фактически и есть решение поставленной задачи, определяющее величину стороны AB = с, и всех остальных сторон, само собой, как функцию неопределенного параметра β. Напомню, что
BC = с*√2, а AC = c*√(3 - 2√2*cos(β)).
Частный случай, когда AC является диаметром, решается элементарно по тому же методу.
В этом случае AEC - прямоугольный треугольник, а ABC - равнобедренный, то есть AC = BC = c√2, а радиус окружности очевидно равен AC/2 = c√2/2 = 5; откуда AB = c = 5√2; BC = AC = 10;
из полученной в задаче формулы этот случай получается, если 2√2*cos(β) = 1; что легко проверить. То есть, когда cos(β) = √2/4; и, соответственно, sin(β) = √14/4;
Другой напрашивающийся частный случай - если угол ABC - прямой. В этом случае cos(β) = 0; sin(β) = 1;
Треугольник получается подобным треугольнику со сторонами (1, √2, √3) при этом меньший катет равен c = 5√6/9; и так далее.
Отдельный вопрос - про область определения.
Так, например, очевидно, что если cos(β) < 0, то решение есть всегда. То есть для тупых углов ABC решение есть всегда. К счастью, 3/2√2 > 1 и 9/4√2 > 1, поэтому решение существует при любых значениях β между 0 и 180 градусами.