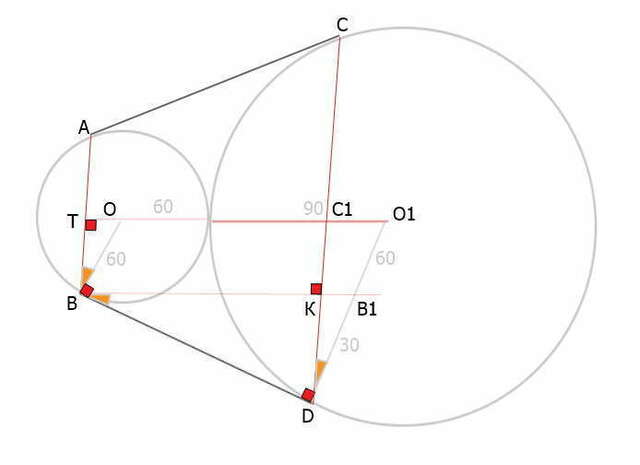
Ключ к решению -- подобие треугольников)))
если провести радиусы в точки касания -- получим прямоугольные треугольники...
если соединить центры окружностей -- получим еще группу прямоугольных треугольников и среди них будут подобные)))
треугольники AOВ и CO1D -- равнобедренные,
ОО1 -- биссектриса угла между касательными к окружностям, т.е. является
и медианой и высотой...
ОО1 _|_ AB и ОО1 _|_ CD
проведем прямую ВВ1 || ОО1
углы АВО = CDO1, т.к. прямые АВ || CD и ТО1 || ВВ1
треугольник ВВ1D -- прямоугольный (по построению))) и
DK _|_ BB1 -- это высота к гипотенузе прямоугольного треугольника))) -- и
она разбивает прямоугольный треугольник на подобные)))
и дальше можно записывать пропорции-отношения из подобия,
но мне больше нравится тригонометрия и я воспользуюсь определением синуса (т.к. треугольники прямоугольные))) -- просто так запись будет короче...
равные углы (на чертеже -- желтый цвет))) обозначу (а)...
sina = DB1 / BB1 = 30 / 150 = 1/5 -- из треугольника BDB1)))
TO = 60*sina = 60 / 5 = 12 -- из треугольника ОТВ)))
С1О1 = 90*sina = 90 / 5 = 18 -- из треугольника О1С1D)))
TC1 = OO1 - C1O1 + TO = 60+90 - 18 + 12 = 150-6 = 144 --это искомое расстояние)))
-----------------можно было и чуть иначе...
искомое расстояние = ВК
зная синус в прямоугольном треугольнике ВКD и вычислив гипотенузу BD (из прямоугольного треугольника BDB1 по т.Пифагора как √(150² - 30²) ))),
можно по основному триг.тождеству записать cosa = √(1 - sin²a)
и ВК = cosa*BD = 2*√6 * 60*√6 / 5 = 12*12 = 144
мне первое решение просто больше нравится)))