8.
m = 1.7x
n = 20\9y
m:n = 2.6
Уменьшая x в несколько раз, мы во столько же раз уменьшаем и соотношение m:n. Увеличивая же y, мы также уменьшаем это соотношение.
3*13\5 = 39\5 - во столько раз уменьшится соотношение.
26\10 делим на 39\5 = 13\39 = 1\3
m = 3x\4
n = 1.5y
m - n = -2.5
в случае с вычитанием надо умножить изменение x или y на соответствующий множитель из m или n, затем вычесть.
35\10 *3\4 - 35\10 * 3\2 = 105\40 - 105\20 = - 105\40 = -21\8
Графики:
Можно строить просто по точкам. Для удобства разбиваем функцию на отрезки, где модуль раскрывается с определенным знаком.
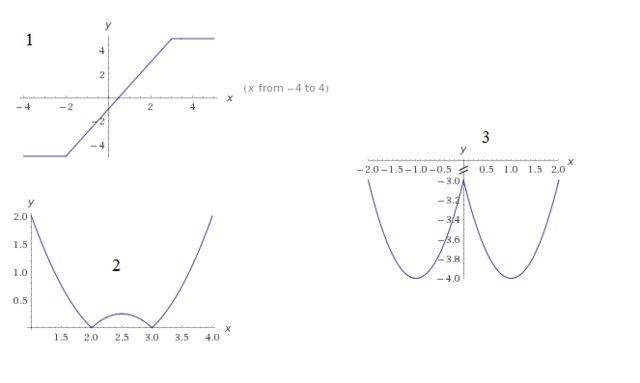
1. f(x) = |x + 2| - |x - 3|
x = -2 и x = 3 - такие точки
при x < - 2
f(x) = - x -2 -3 + x = -5
при -2 <= x <= 3<br>f(x) = x + 2 - 3 + x = 2x - 1
при x > 3
f(x) = x + 2 - x + 3 = 5
2. f(x) = |x^2 - 5x + 6|
x1 + x2 = 5
x1*x2 = 6
x1 = 3, x2 = 2
+ 2 - 3 +
при x < 2 и x > 3
f(x) = x^2 - 5x + 6 - обычная парабола
при 2 <= x <= 3 <br>f(x) = -x^2 + 5x - 6 - также обычная ппарабола, но перевернутая.
Можно поступить проще. Построить сначала параболу f(x) = x^2 - 5x + 6, а затем отобразить все, что ниже оси - вверх.
3. f(x) = x^2 - 2|x| -3
при x >= 0
f(x) = x^2 - 2x -3
иначе
f(x) = x^2 + 2х -3
Две половинки разных парабол