Решение:
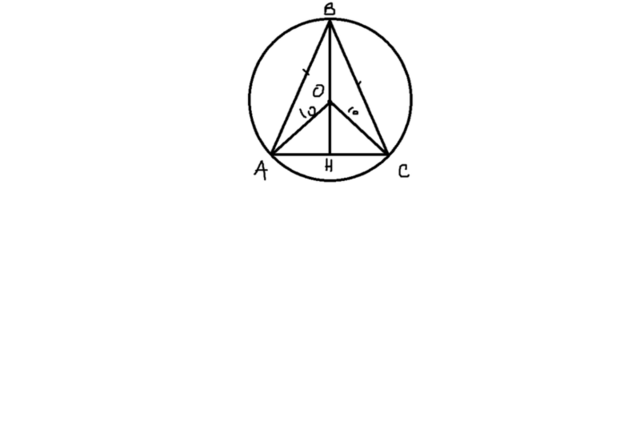
1) а) Радиус описанной окружности около треугольника - расстояние серединного перпендикуляра от концов отрезка. Известно, что радиус равен 10 сантиметрам.
(см. рис. 1). Очевидно, из рисунка видно, что оставшаяся часть BO также является радиусом, равным 10 см. OH = 16-10=6 (см).
Рассматриваем маленький прямоугольный треугольник ΔOHA. Мы знаем его гипотенузу и катет. Нам остается только применить т. Пифагора:

Поскольку высота в равнобедренном треугольнике является медианой, то AH=HC=6 см. Вся часть, очевидно, равна 12 см.
Площадь равна полупроизведению основания на высоту. Поэтому,

см².
б) Рассмотрим треугольник ΔBHA. Нам надо найти гипотенузу, используя два известных катета. Применяем теорему Пифагора:

см.
Ответ: а) 96 см². б) 2√73 см
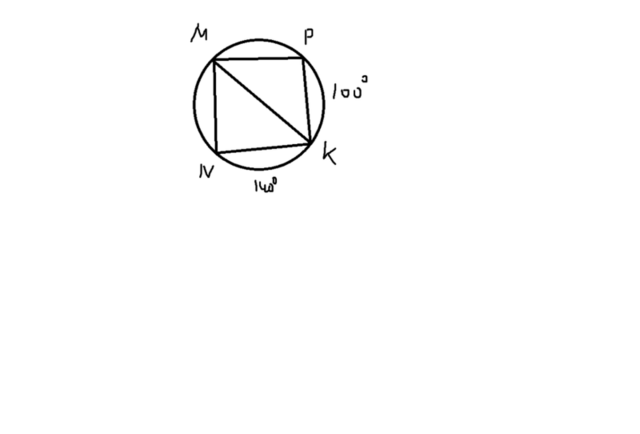
2) Угол MNK опирается прямо на дугу, следовательно, этот угол будет составлять половину от 180 градусов, т.е. угол MNK равен 90. Раз четырехугольник вписан в окружность, а по свойству вписанного четырехугольника в окружность, угол MNK будет равен углу MPK, т.е. также 90 градусов.
Найдем, чему будет равен угол MNP. Этот угол опирается на дугу PKN, градусная мера которой равна сумме 100 и 140, т.е. 240 градусов. Угол MNP будет составлять половину от этой градусной меры, т.е. 120 градусов. Отсюда мы найдем, что последний угол будет равен 60 градусов.
Ответ: 90,90,60,120