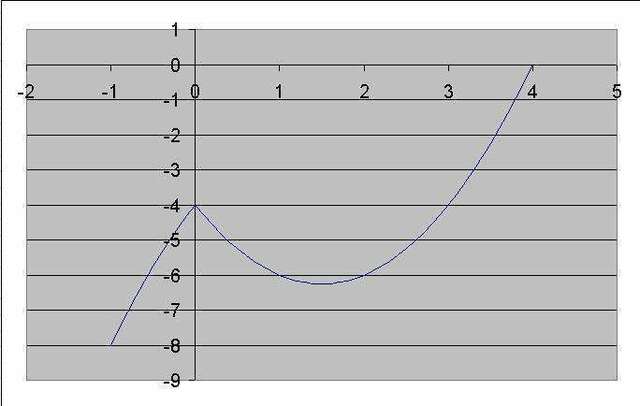
Рассмотрим функцию у=|x|(x-3)-4
при x >= 0 у=x*(x-3) -4 - парабола с минимумом в точке (1,5;-6,25)
при x < 0 у=-x*(x-3) -4 - ветвь параболы
график у=|x|(x-3)-4 приведен во вложении
пересечение графика у=|x|(x-3)-4 с горизонтальной прямой у=b возможно в нескольких точках
1) при b < -6,25 - в одной точке
2) при b = -6,25 - в двух точках
3) при -6,25 < b < -4 - в трех точках
4) при b = -4 - в двух точках
5) при b > -4 - в одной точке
ответ:
количество решений уравнения |x|(x-3)-4=b зависит от параметра b
1) при b < -6,25 - одно решение
2) при b = -6,25 - два решения
3) при -6,25 < b < -4 - три решения
4) при b = -4 - два решения
5) при b > -4 - одно решение
**************
замечание 1
в ответе случай 2) и 4) можно объединить
замечание 2
в ответе случай 1) и 5) можно объединить