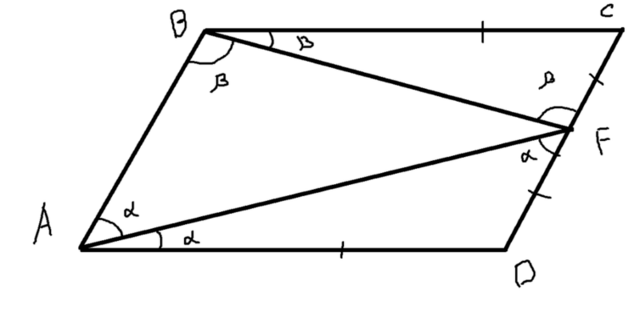
Cм. рисунок.
Так как по условию это биссектрисы, то:
1) (угол) BAF=FAD а также FBC=FBA
2) (угол) FAD=AFD (При параллельных прямых AB и CD и секущей AF)
Так как эти углы равны, значит треугольник ADF - равнобедренный, поэтому стороны AD и DF равны.
3) (угол) ABD=BFC (При параллельных прямых AB и СD и секущей BF)
Так как и эти углы равны, значит треугольник DCF - равнобедренный, поэтому стороны BC=CF.
Известно, что у параллелограмма AD=BC, тогда AD=DF=FC=CB.
Тогда F - середина CD, что и требовалось доказать.