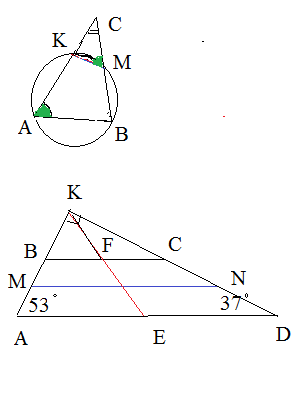
1) Четырехугольник АКMB вписан в окружность. Сумма противоположных углов такого четырехугольника равна 180°:
∠ КАВ
+∠КМВ =180° ⇒
∠
KMB =180°-
∠ KAB
Тогда смежный с ним угол ∠KMС = 180° -∠KMB =180°- (180°-
∠
KAB) =
∠ KAB
Угол С- общий.
Треугольники подобны по двум углам.
2) Продолжим боковые стороны трапеции до пересечения в точке К, так как углы прилежащие к основанию AD равны 53° и 37°, что в сумме составляет 90°, то
∠ AKD - прямой.
По условию MN=21 cм и MN- средняя линия трапеции, соединяет середины боковых сторон.
FE=12 cм
Значит КЕ - медиана прямоугольного треугольника АКВ и она равна половине гипотенузы, AD=2KE.
КF- медиана прямоугольного треугольника ВКС и ВС=2KF.
Обозначим KF=x, тогда ВС=2х
КЕ=х+12, AD=2(x+12)=2x+24
MN=(BC+AD)/2
Составим уравнение:
21=(2x + 2x+24)/2,
42=4х+24,
4х=18
2х=9
ВС=2х=9
AD=2x+24=9+24=33
Ответ. Основания трапеции 9 см и 33 см.