Хорошая задача!!
из серии "как нетрудно догадаться")))
первая мысль, которая должна бы появиться: раз есть окружность -- нужно искать углы...вписанные и центральные... искать равные углы...
искать дуги, на которые углы опираются...
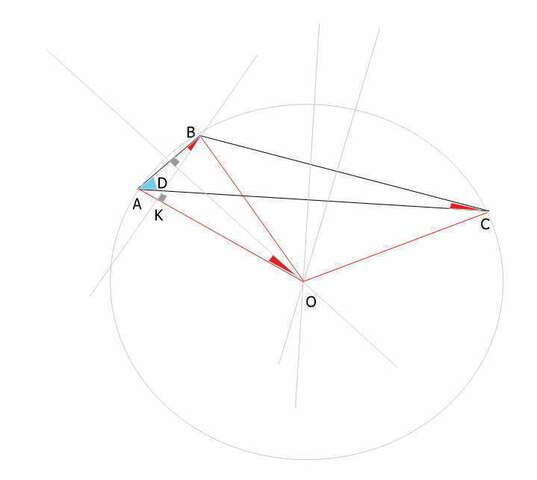
центр описанной окружности = точка пересечения серединных перпендикуляров к сторонам треугольника)))
треугольник ВОА равнобедренный по построению и серединный перпендикуляр к стороне ВС -- это биссектриса=медиана=высота)))
угол ВОА -- центральный, опирающийся на дугу ВА,
угол ВСА -- вписанный, опирающийся на ту же дугу)))
вывод: ВОА = 2*ВСА
в равнобедренном треугольнике ВОА -- ВК это высота (по условию))) и
серединный перпендикуляр к основанию -- тоже высота))
получили два прямоугольных треугольника с общим углом ВАО ))))))))
значит третьи углы в этих треугольниках равны)))
угол АВК будет равен половине угла АОВ: АОВ = 2*АВК,
т.е. ВСА = АВК
а теперь если вернуться к данному треугольнику АВС, то "нетрудно заметить",
что треугольники АВС и АВD -- подобны)))))
у них угол ВАС -- общий, и два острых угла равны: АВD = ВСА
запишем пропорцию:
АВ / АС = AD / AB
AD = AB*AB / AC = 8*8 / 64 = 1
CD = 64 - 1 = 63