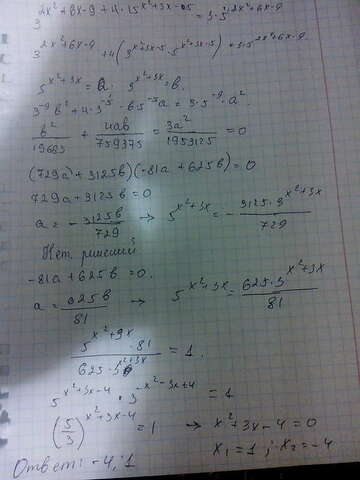Помогите пожалуйсто решить

$3*16^x+37*36^x=26*81^x$
Воспользуемся свойством степеней
$3(4^2)^x+37(4*3)^x=26(9^2)x \\ 3*4^2^x+37*4^x*9^x=26*9^2^x$
Пусть $9^x=a;4^x=b$
$3b^2+37ba=26a^2 \\ 37ab+3b^2-26a^2=0$
Производим группировку
$(13a+b)(-2a+3b)=0$
$13a+b=0 \\ b=-13a \\ 4^x+13*9^x=0$
Нет решений
$-2a+3b=0 \\ a= \frac{3b}{2} \\ 9^x= \frac{3*4^x}{2} \\ ( \frac{3}{2} )^2^x^-^1=1 \\ 2x-1=0 \\ x=0.5$

Ответ: 0,5

Второе уравнение во вложение

3. ОДЗ

0} \atop {x+1>0}}\atop {x^3-9x+8>0} \right. " alt=" \left \{ {{x-1>0} \atop {x+1>0}}\atop {x^3-9x+8>0} \right. " align="absmiddle" class="latex-formula">
Воспользуемся формулами перехода к новому основанию логарифма
$log_x_+_1(x^3-9x+8)= \frac{3}{ \frac{log_x_+_1(x+1)}{log_x_+_1(x-1)} } \\ log_x_+_1(x^3-9x+8)= 3: \frac{log_x_+_1(x+1)}{log_x_+_1(x-1)} \\$
Переворачиваем дробь
$log_x_+_1(x^3-9x+8)=\frac{3log_x_+_1(x-1)}{log_x_+_1(x+1)} \\ log_x_+_1(x^3-9x+8)=\frac{3log_x_+_1(x-1)}{1}$
$log_x_+_1(x^3-9x+8)=3log_x_+_1(x-1)$
Воспользуемся свойством логарифмов
$log_x_+_1(x^3-9x+8)=log_x_+_1((x-1)^3)$
$x^3-9x+8=(x-1)^3$
Раскрываем скобки
$x^3-9x+8=x^3-3x^2+3x-1 \\ x^2-4x+3=0$
Находим дискриминант
$D=b^2-4ac=(-4)^2-4*1*3=4; \sqrt{D} =2$
Дискриминант положителен значит уравнение имеет 2 корня
$x_1= \frac{4-2}{2*1} =1;x_2= \frac{4+2}{2*1} =3$
$x=1$ - не удовлетворяет ОДЗ

Ответ: $x=3$