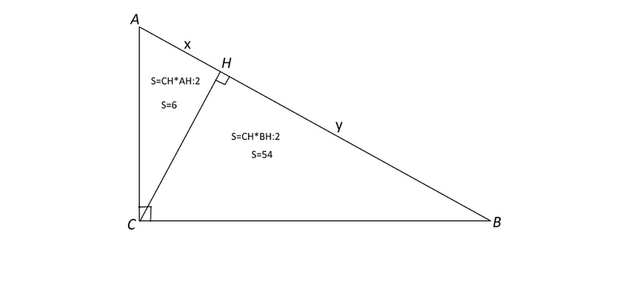
Пусть этот прямоугольный треугольник будет АВС с прямым углом С,
а высота к гипотенузе СН.
Обозначим отрезок АН=х
НВ=у
Тогда S(AHC)=АН*СН:2=6,
откуда СН=6*2:х
Из треугольника СНВ
СН=54*2:у
Катет СН в обоих треугольниках один и тот же, следовательно
12:х=108:у
12у=108х
у=9х
Самое время вспомнить, что высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;
СН²=АН*ВН=х*9х=9х²
СН=3х
Из тр-ка АНС
S=3x*x:2
12=3x²
х²=4
х=2
АВ=АН+НВ=10х
АВ=10*2=20
Проверка:
Площадь АВС=6+54=60
СН=3х=6
S(ABC)=CH*AB:2=6*20:2=60