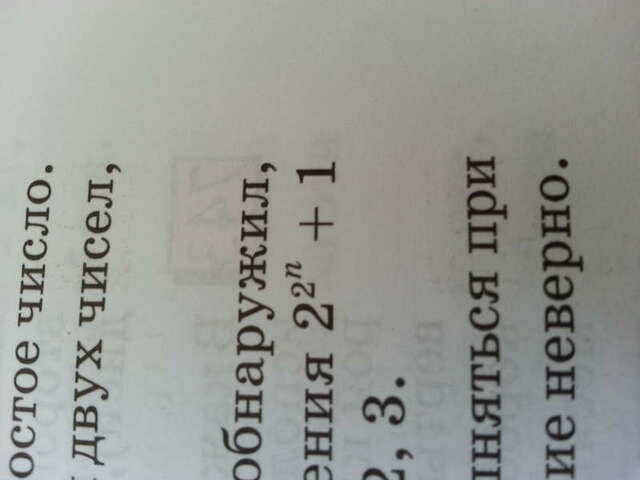Помогите пожалуйста.
1)Французкий математик Пьер Ферма, живший в XVII веке, обнаружил, что при небольших натуральных значениях n значение выражения (смотр на рис. 1) является простым числом. Проверь это утверждение для n=1,2,3.
2)Пьер Ферма поставил вопрос о том, будет ли это свойство выполняться при любых n. Позже выяснилось, что в общем виде данное утверждение неверно. Как ты думаешь, каким способом это было доказанно ?
рис.1 снизу