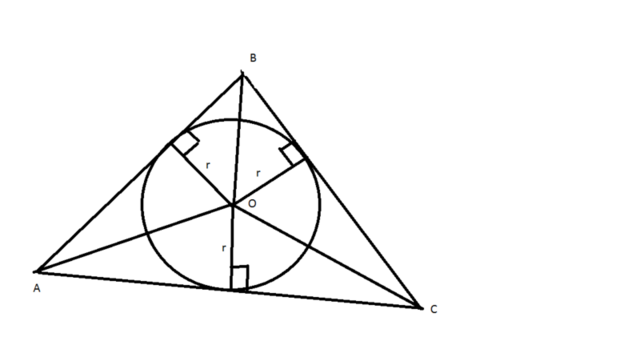
Тк Центр вписанной окружности точка пересечения его бессектрис,то
AO ,BO,CO бессектрисы углов A B C. Тогда если r радиус окружности,то
AO=r/sinA/2 BO=r/sinB/2 CO=r/sinС/2
Тк все углы A/2 B/2 С/2 острые тк (положим что есть тупой угол 180 >F ,то F/2<90)<br> То при возрастании угла его синус возрастает и наоборот.
Наикратчайшим(наименьшим) из расстояний AO BO CO является то ,где синус половинного угла будет наибольшим. А значит половинный угол самый большой. А значит самый большой и сам угол. Как мы знаем наибольший угол лежит против наибольшей стороны. То есть на против стороны AC-угол B,а значит наш угол
B,наткратчайшее расстояние BO
Ответ: ближе всего к вершине B