7sin^2x+cos^2x=5sinx
7sin^2x + 1
- sin^2x - 5sinx = 0
6sin^2x -
5sinx + 1 = 0
Пусть sinx
= t, t ∈ [ - 1; 1], тогда
6t^2 - 5t + 1 = 0
D = 25 - 24 = 1
t1 = ( 5 + 1)/12 = 6/12 = 1/2
t2 = ( 5 –
1)/12 = 4/12 = 1/3
sinx = 1/2
;
x = pi/6 +
2pik
x = 5pi/6 +
2pik, k ∈ Z
sinx = 1/3
x = (-1)^k * arcsin (1/3) + pik
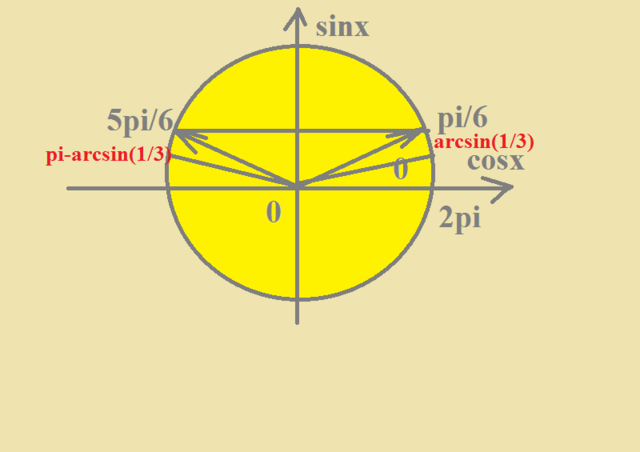
+ ОТБОР на фото
arcsin(1/3) ;
pi/6 ;
5pi/6;
pi - arcsin(1/3)