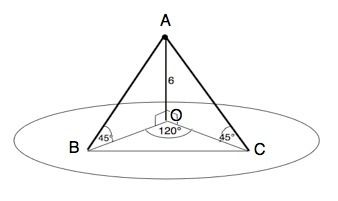
Из точки, удаленной от плоскости на 6 см, проведены две наклонные. Найдите расстояние между основаниями наклонных, если угол между их проекциями равен 120°, а каждая наклонная образует с плоскостью угол 45°.
Расстояние от точки до плоскости - длина отрезка, проведенного из точки к плоскости перпендикулярно.
Обозначим наклонные АВ и АС, расстояние от А до плоскости– АО, перпендикулярно ей и равно 6
∠АВО=∠АСО= 45° , АО - общий катет прямоугольных ∆ АОВ и ∆ АОС, ⇒ они равны, второй острый угол равен 45°, ⇒ ∆ АОВ=∆АОС равнобедренные, и проекции наклонных
ВО=СО=6 см.
Соединив основания наклонных, получим равнобедренный треугольник ВОС.
∠ВОС=120°, ⇒ ∠ОВС=∠ОСВ=(180°-120°):2=30°.
По т.синусов
ВС:sin120°=OB:sin30°

BC=2OB√3
BC=OB√3=6√3 см
---------------
ВС можно найти иначе:
а) провести из О высоту (медиану, биссектрису) к ВС, по т.Пифагора найти половину ВС, и затем ВС полностью.
б) найти ВС по т.косинусов.