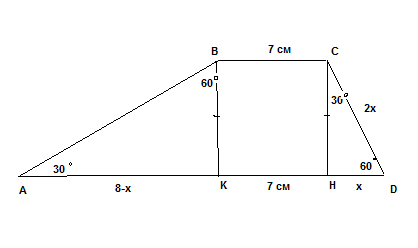
Трапеция АВСD: ВС=7, AD=15. 
Найти ВК=СН
Решение. АК+HD=15-7=8
Обозначим HD=x, тогда АК=8-х.
Из прямоугольного треугольника CHD: CD=2HD=2x,
катет, лежащий против угла в 30° равен половине гипотенузы, значит гипотенуза в два раза больше катете.
По теореме Пифагора СН²=CD²-HD²=(2x)²-x²=3x²,
CH=x√3
ВК=СН=х√3
Рассмотрим прямоугольный треугольник АВК: АВ=2ВК=2х√3 .
Катет, лежащий против угла в 30° равен половине гипотенузы, значит гипотенуза в два раза больше.
Применяем теорему Пифагора:
АВ²=АК²+ВК²
или
(2х√3)²=(8-х)²+(х√3)²,
12х²=64-16х+х²+3х²,
х²+2х-8=0,
D=2²-4(-8)=4+32=36
x=(-2-6)/2=-4 - не удовлетворяет условию задачи
или
х=(-2+6)/2=2
HD=2 см, СН=2√3 см
АК=8-2=6 см
Диагональ BD находим по теореме Пифагора из прямоугольного треугольника ВКD: ВК=2√3, КD=KH+HD=7+2=9
BD²=BK²+KD²=(2√3)²+9²=12+81=93
BD=√93,
Диагональ АС найдем из прямоугольного треугольника АСН: АН=АК+КН=6+7=13 см,
АС²=АН²+СН²=13²+(2√3)²=169+12=181
АС=√181
Ответ высота трапеции 2√3, диагонали √93 и √181