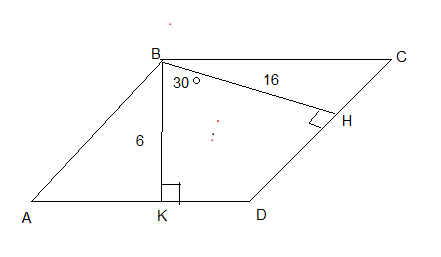
Cумма углов четырехугольника BKDH равна 360°, Найдем тупой угол D параллелограмма:

Сумма углов параллелограмма, прилежащих к одной стороне равна 180°.Значит угол А равен 180°-150°=30°
Рассмотрим прямоугольный треугольник АВН. Катет ВН=6, лежащий против угла в 30° равен половине гипотенузы АВ, значит гипотенуза АВ равна 12 см.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
S= CD·16, СВ=АВ=12 см
S=12·16=192 кв.см