Основа рівнобедреного тупокутного трикутника дорівнює 18 см, а радіус описаного навколо...

0 голосов
197 просмотров

Основа рівнобедреного тупокутного трикутника дорівнює 18 см, а радіус описаного навколо нього кола -- 15 см. Знайдіть бічну сторону трикутника.

Геометрия | 197 просмотров
Дано ответов: 2
0 голосов
Правильный ответ

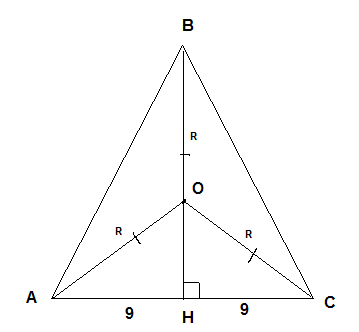
ОА=ОВ=ОС=R=15 см
В равнобедренном треугольнике высота ВН- медиана, значит АН=НС=9 см.
По теореме Пифагора из прямоугольного треугольника АОН:
ОН²=АО²-АН²=15²-9²=225-81-144=12 см
ВН=ВО+ОН=15+12=27 см
По теореме Пифагора из прямоугольного треугольника АВН:
АВ²=АН²+ВН²=9²+27²=9²+3²·9²=9²(1+9)=9²·10
АВ=9·√10
Ответ 9√10- длина боковой стороны.

image
(413k баллов)
0 голосов

У меня есть только одна формула, которая там где я учусь в лицеи

b= \sqrt{2R^2+ \sqrt{4R^4-R^2a^2} } = \sqrt{2*15^2+ \sqrt{4*15^2-15^2*18^2} } =9\sqrt{10}

Похожие задачи