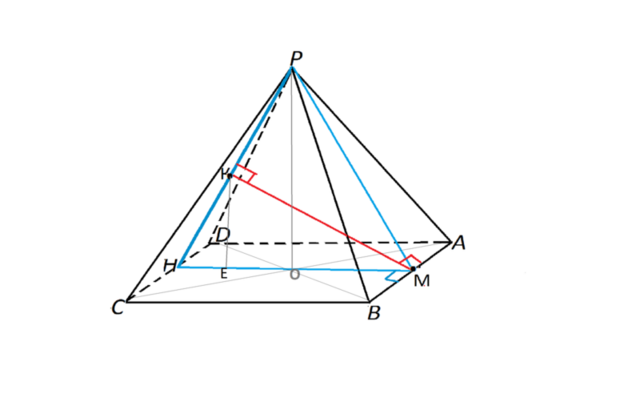
Основание правильной четырехугольной пирамиды - квадрат.
Сторона основания равна апофеме РН, следовательно,
средняя линия НМ квадрата ABCD тоже равна РН.
Боковые грани - равнобедренные треугольники, и апофема РМ
равна апофеме РН.
Основание высоты РО пирамиды - в точке пересечения диагоналей квадрата, высота перпендикулярна основанию, отсюда
сечение РНМ, содержащее эту высоту, перпендикулярно основанию,
а стороны треугольника НРМ равны.
∆ НРМ -
правильный.
НМ перпендикулярна АВ, отсюда
КМ перпендикулярна АВ,
т.к. НМ содержит ее проекцию ЕМ, перпендикулярную АВ ( теорема о 3-х перпендикулярах).
⇒ высота
КМ правильного треугольника КРН в то же время
общий
перпендикуляр между РН и АВ
Углы ∆ НРМ равны 60°
∠КНМ=60°,
КМ=НМ*sin*(60°)= 4√3*(√3)
:2=
6