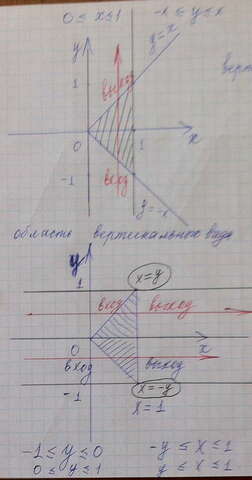
Смотрим на данный двойной интеграл. У первого интеграла переменная интегрирования х. Нижний предел 0 можно записать в виде уравнения х=0 - линия, ограничивающая область интегрирования слева. Верхний предел 1, уравнение линии, ограничивающей область справа: х=1.
У второго интеграла переменная интегрирования у, нижний предел -х, значит уравнение линии, ограничивающей область снизу : у=-х,
верхний предел х, значит уравнение линии, ограничивающей область сверху: y=х.
Область интегрирования расположена в вертикальной полосе между прямыми х=0 и х=1. Поэтому она называется областью вертикального вида. Проведем прямую (красный цвет) параллельную границам. Входим в область в направлении оси оу.
Линия входа (снизу) у=-х, линия выхода у=х.
Теперь представим эту же область как область горизонтального вида (см рисунок внизу)
Область должна находиться внутри горизонтальной полосы. Таких полос две.
Одна, ограничена линиями у=-1 и у=0, линия входа х=-у( получаем из уравнения у=-х, выразив переменную х), линия выхода х=1
Вторая область ограничена полосой : у=0, у=1, линия входа х=у ( получили из уравнения у=х, выразив переменную х), линия выхода такая же х=1
Области записаны в виде неравенств ниже второго рисунка.
Oбластей горизонтального вида две, у них разные линии входа, внизу х=-у, а вверхней области х=у
Ответ (2)
2 задача, ответ2. Проверка. (-1/3 сos (3х+5)) `=-1/3 ·(- sin (3x+5))·(3x+5)`=sin (3x+5)