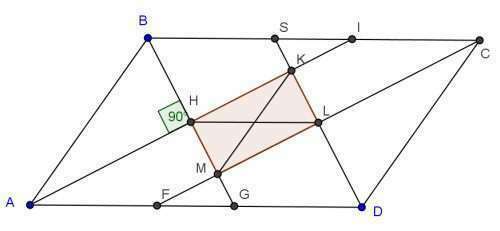
Согласно свойств биссектрисы параллелограмма:
1) биссектриса отсекает от параллелограмма равнобедренный треугольник (по
свойству накрест лежащие углы равны, а так как биссектриса делит угол на две
равные части, то все углы, касающиеся биссектрисы, равны): например, ΔВАG в нем АВ=AG.
2) биссектрисы параллелограмма ABCD, пересекаясь, образуют прямоугольник HKLM, потому что биссектрисы смежных углов
пересекаются под прямым углом:;
Рассмотрим Δ ВАG и ΔSCD они равны (противолежащие стороны и углы параллелограмма равны) и являются равнобедренными, а
потому биссектрисы АН и CL являются одновременно и медианами, и высотами.
Следовательно, HG=LD, кроме того, НG||LD
(биссектрисы противоположных углов параллелограмма параллельны), поэтому четырехугольник GHLD- параллелограмм, а тогда HL||GD
и HL=GD.
НL и KM является диагоналями прямоугольника НКLM, а диагонали прямоугольника равны.
HL= GD = AD- АВ= 11-8=3.