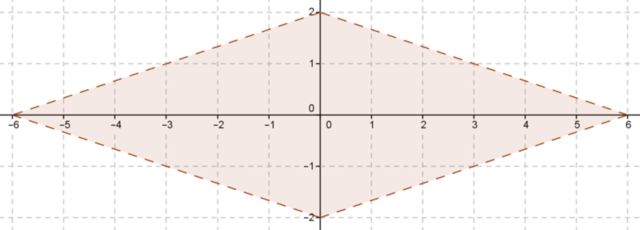
При x >= 0, y >= 0 легко раскрыть модули: |x| + 3|y| - 6 = x + 3y - 6 < 0. С учетом ограничений на x, y получаем треугольник с вершинами (0,0), (6,0), (0,2). Т.к. неравенство переходит само в себя при всяких заменах знаков x, y, то искомое множество можно получить, отражая получившийся треугольник относительно осей и начала координат. Результат - внутренность ромба с выколотой границей.
Количество целых точек можно подсчитать непосредственно по рисунку, их 21.