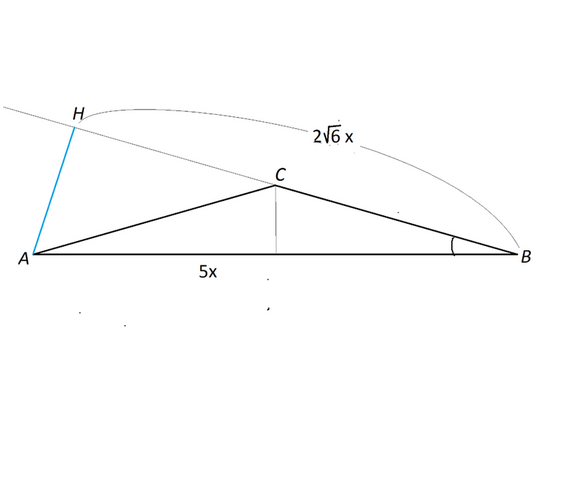
В треугольнике ABC стороны AC и BC равны, AH - высота, cos ∠BAC = (2√6):5. Найти cos ∠BAH
В треугольнике АСВ углы при основании АС равны. ∠А=∠В, ⇒cos ∠BAC=cos CBА=sin ∠HAB
cos ∠BAH=АН:АС
Катет в отношении прилежащей к углу стороны к гипотенузе
2√6=4,8989, т.е почти равен гипотенузе.
Следовательно,
угол С тупой и высота АН расположена вне треугольника.
Сделаем рисунок
Пусть
гипотенуза АС прямоугольного треугольника НАС будет
5х,
катет
НВ=
2√6 х
Тогда катет
АН по т.Пифагора равен √(АС²-ВН²)
=1
cos ∠BAH=АН:АС=1:5=0,2