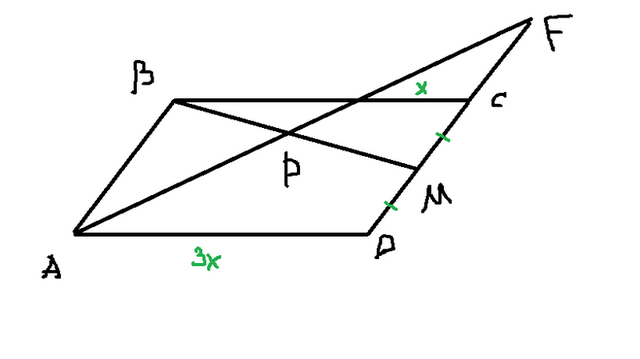
Пока только BP/PM, но посижу еще со второй частью ответа (хотя бы одна будет).
Достроить PN до пересечения с CM. Тогда Для треугольника BCM и секущей PF записывается теорема Менелая:
 (1)
(1)
AD/NC = DF/CF= 3 (подобные треугольники), то CF/FM = 1/2. Чтобы было яснее, возьмите, например, CF=m. Тогда DF=3m. Но тогда на равные части приходится еще по m. BN/NC = 2/1. Тогда, подставив в (1), получим MP/PB=1. То есть они равны.
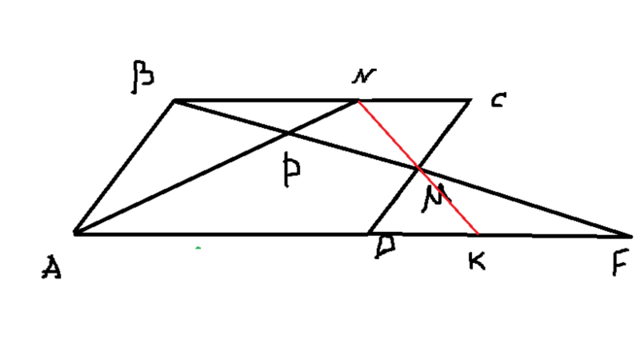
Второй вариант по тому же принципу, правда посложнее немного. Принцип тот же. Треугольник ANK, секущая PF. Запишем теорему Менелая:
 (2)
(2)
Сразу хочется отметить, что треугольники NCM и DMK равны (сторона, два угла), поэтому NM/MK=1. Остается KF/AF. Перечислю свои рассуждения в строчку:
NC=x=DK, AD=3x. Рассмотрим пару подобных треугольников: ABF и DMF (по трем углам). То есть AF/DF=AB/DM=2. Теперь "поиграем" с отношением:
AF/DF=(AD+DK+KF)/(DK+KF)=(4x+KF)/(x+KF)=2. Отсюда KF=2x, AF=6x. Подставим в (2). Получится AP/PN=3.