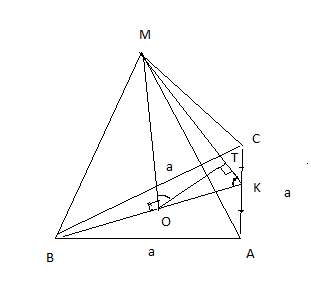
Дана пирамида МАВС, Δ АВС- правильный: АВ=ВС=АС.
Пусть АВ=ВС=АС=а,
Площадь равностороннего треугольника S=1/2·a·а·sin 60⁰=a²√3/4
МО- высота пирамиды, O- центр описанной окружности.
В равностороннем треугольнике центр описанной и центр вписанной окружности совпадают, поэтому ВО=R, OK=r
Так как S=p·r, выразим r через а:
r=a²√3/4 : (а+а+а)/2=а²√3/6.
Проведем апофему МК. МК перпендикулярна АС по теореме о треёх перпендикулярах, так как ОК перпендикуляр к АС.
Рассмотрим прямоугольный треугольник МОК, проведем перпендикуляр ОЕ.
Угол МОЕ=β. Треугольники МОЕ и МОК - прямоугольные, угол ОМК -общий. Значит треугольники подобны по двум углам.
Угол ОКМ =β, tg OKM=MO/OK
MO=OK·tgβ=a√3·tgβ/6
Тогда объём пирамиды
V=1/3· S·MO=1/3 · a²√3/4 · а√3 ·tg β/6=a³·tgβ /24
Так как V известен, то выразим а через V и tg β
a=∛(24·V/ tgβ)
Подставим найденное значение а в выражение площади через сторону а:
S=a²√3/4=∛(24·V/tgβ)² ·√3/4, так как ∛(24)²=4·∛9, то ответ упрощается;
S=√3·∛9V²/tg²β